Qubit Networks
Quantum computers generally have at least two defining features: a good quantum memory for uploading, storing, and retrieving quantum information; and a quantum information bus to manipulate and make gates between quantum memories. Most experiments in trapped ions use the coulomb force between trapped ions as a quantum information bus and so far have been limited to fairly small systems. Our research deals with networking these small systems together to form a quantum system with a large number of qubits. We use photons (in addition to phonons) as a quantum information bus to connect different ion traps (nodes) by interfering photons emitted from ions in separate nodes on a beam splitter as in the above picture. The use of a cross connect switch can reconfigure the connections of the quantum network to entangle atoms from any one ion trap to any other ion trap.
A paper outlining this quantum computing architecture can be found here.
Entangling Remotely Trapped Atoms
Trapped ion quantum bits can be linked through a photonic quantum channel, creating long-distance entanglement between quantum memories, quantum networks, and distributed quantum computers. We create atom-photon networks using a combination of probabilistic atom-photon entanglement together with deterministic atom-atom entanglement. Ions and photons make an ideal pair for a quantum network which needs both stationary memory qubits and flying communication qubits. The long coherence times of trapped ions make them stand out as the state of the art quantum memory and the fast speed at which photons travel make them the ideal candidate for communication qubits.
In order to entangle two remote ions, each ion is first entangled with an emitted photon degree of freedom such as frequency or polarization. Direct entanglement between “stationary” (ion) and “flying” (photon) qubits was first observed in our lab in 2004 (Nature 428, 153 (2004)).
The single photons from ions in separate traps are collected and directed to a 50:50 beamsplitter. Due to the quantum interference of the photons (Nature Physics 3, 538 (2007)), detection of certain Bell states of light upon exiting the beam splitter projects the atoms into an entangled state. For example, only an antisymmetric photonic state will result in a simultaneous detection at both output ports of the beamsplitter. It is this “double-click” of the detectors that heralds the entanglement of the two ions. Thus, it is the simultaneous destruction of the photons that lets us know that the ions are now entangled (Nature 449, 68 (2007)).
The single photons from ions in separate traps are collected and directed to a 50:50 beamsplitter. Due to the quantum interference of the photons (Nature Physics 3, 538 (2007)), detection of certain Bell states of light upon exiting the beam splitter projects the atoms into an entangled state. For example, only an antisymmetric photonic state will result in a simultaneous detection at both output ports of the beamsplitter. It is this “double-click” of the detectors that heralds the entanglement of the two ions. Thus, it is the simultaneous destruction of the photons that lets us know that the ions are now entangled (Nature 449, 68 (2007)).
This entanglement between distant ions was used to carry out a teleportation protocol (Science 323, 486 (2009): the first experiment to demonstrate quantum teleportation between atomic qubits separated by a macroscopic distance), and to carry out heralded quantum gates between remotely trapped atoms (PRL 102, 250502 (2009)). In the teleportation experiment, it took about 10 minutes to teleport one quantum bit of information owing to the low photon collection probability.

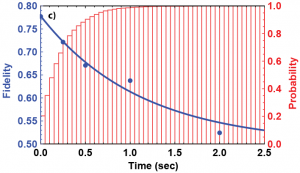
Our efforts now involve decreasing the time required to generate entanglement between remote ion traps. In order to make a practical quantum network, generating entanglement faster than entanglement decoheres is important. Currently, we use high NA optics to collect a much larger percentage of the solid angle of light. We also detect two Bell states of light after the beam splitter rather than one. Using these improvements, we now generate entanglement at a rate of 2 – 5 Hz instead of 2 mHz. The time to generate entanglement is less than the single atom coherence time and likely less than the remote entangled state lifetime. The graph below shows phase coherence between remote atoms at an entanglement rate of 3 Hz (preliminary data). This rate is faster than the measured decoherence rate of our remotely entangled ions. Passing this threshold is crucial for scaling this system. The resource scaling is combinatoric (worse than exponential) if the time required to generate entanglement is more than the coherence time of the qubits. Trapped ions are the only platform so far to cross this threshold.
Atom Entanglement in One Node
Deterministic entangling operations in trapped ion systems are carried out by using “spin-dependent” forces which couple the internal states of the individual ions to the collective motion shared among nearby ions. Traditionally, these operations are carried out using continuous wave lasers, but our group has been able to simplify these procedures by using an industrial mode-locked pulsed laser at 355 nm. In the regime where many pulses are needed to flip the qubit state of the ion, a train of pulses creates an optical frequency comb. The large bandwidth and spectral purity of the optical frequency comb can be used to drive Raman transitions between qubit levels and address an ion chain’s normal modes of motion. By addressing these motion and spin degrees of freedom, it is possible to deterministically entangle neighboring ions and probe their coherence using the simplicity of a frequency comb (PRL 104, 140501 (2010)).
We have also developed a method for suppressing common errors (PRL 109, 020503 (2012)) in spin dependent force quantum gates by simple pulse shaping. By flipping the RF phase of an AOM by 180 degrees at prescribed times, we push error in quantum gates between adjacent ions to higher order. In theory, detuning and timing errors can be suppressed to arbitrary order in quantum gates where spin is coupled to harmonic oscillator modes at the expense of increasing gate time.
In addition to pulse shaping a frequency comb to create entanglement between adjacent ions, we can create entanglement that is insensitive to the optical phase of the frequency comb. This allows us to sync the phase of the entangled state across modules by locking the microwave beatnote of the Raman beams to an external clock. Synchronizing entangled phases between ion traps will be important in a scaled-up system. We outline and demonstrate such a system here.
Putting it together: entanglement using photons and phonons
We have recently demonstrated entanglement across and within ion traps using photons and phonons. We entangled remotely trapped atoms using photons in two separate ion traps, followed by entangling atoms in the same trap using phonons as a quantum bus. The results of this experiment can be found in our new paper on the arXiv.
Current People:
George Toh – Post Doc (2019-)
Ksenia Sosnova – Graduate Student (2014-)
Allison Carter – Graduate Student (2016-)
Jameson O’Reilly – Graduate Student (2019-)
Sagnik Saha – Graduate Student (2020-)
Alumni:
Leeza Moldavchuk- Undergraduate Student
Sophia Scarano- Undergraduate Student
Martin Lichtman- Post Doc
Clayton Crocker- Graduate Student
Volkan Inlek- Graduate Student
David Hucul- Graduate Student
Grahame Vittorini- Post Doc
Susan Clark- Post Doc
David Hayes- Graduate Student
Kenny Lee- Undergraduate Student
Qudsia Quraishi- Post Doc
Steven Olmschenk- Graduate Student
Dzmitry Matsukevich- Post Doc
Peter Maunz- Post Doc
David Moehring- Graduate Student
Boris Blinov- Post Doc
RELEVANT PAPERS:
“High Purity Single Photons Entangled with an Atomic Memory,” C. Crocker, M. Lichtman, K. Sosnova, A. Carter, S. Scarano, and C. Monroe, Optics Express Vol. 27, Issue 20, pp. 28143-28149 (2019).
“Multispecies Trapped-Ion Node for Quantum Networking,” I. V. Inlek, C. Crocker, M. Lichtman, K. Sosnova, and C. Monroe, Phys. Rev. Lett. 118, 250502, (2017). [Supplemental Material]
“Modular Entanglement of Atomic Qubits using Photons and Phonons,” D. Hucul, I.V. Inlek, G. Vittorini, C. Crocker, S. Debnath, S.M. Clark, and C. Monroe, Nature Physics 11, 37-42 (2015).
“Entanglement of distinguishable quantum memories,” G. Vittorini, D. Hucul, I.V. Inlek, C. Crocker, and C. Monroe, Phys. Rev. A 90, 040302(R) (2014).
“Quantum Gates with Phase Stability over Space and Time,” I.V. Inlek, G. Vittorini, D. Hucul, C. Crocker, and C. Monroe. Phys. Rev. A 90, 042316 (2014).
“Coherent Error Suppression in Multiqubit Entangling Gates,” D. Hayes, S. M. Clark, S. Debnath, D. Hucul, I. V. Inlek, K. W. Lee, Q. Quraishi, and C. Monroe, Phys. Rev. Lett. 109, 020503 (2012).
“Entanglement of Atomic Qubits Using an Optical Frequency Comb,” D. Hayes, D. N. Matsukevich, P. Maunz, D. Hucul, Q. Quraishi, S. Olmschenk, W. Campbell, J. Mizrahi, C. Senko, and C. Monroe, Phys. Rev. Lett. 104, 140501 (2010).
Review: “Quantum Logic Between Distant Trapped Ions,” S. Olmschenk, D. Hayes, D. N. Matsukevich, P. Maunz, D. L. Moehring, and C. Monroe, Int. J. Quant. Inf. 8, 337 (2010)
Review: “Protocols and Techniques for a Scalable Atom–Photon Quantum Network,” L. Luo, D. Hayes, T.A. Manning, D. N. Matsukevich, P. Maunz, S. Olmschenk, J. D. Sterk, and C. Monroe, Fortschr. Phy. 57,11-12 (2009).
“Heralded Quantum Gate Between Remote Quantum Memories,” P. Maunz, S. Olmschenk, D. Hayes, D. Matsukevich, L.-M. Duan and C. Monroe, Phys. Rev. Lett. 102, 250502 (2009).
“Quantum Teleportation Between Distant Matter Qubits,” S. Olmschenk, D. Matsukevich, P. Maunz, D. Hayes, L.-M. Duan and C. Monroe, Science 323, 486 (2009).
“Bell Inequality Violation with Two Remote Atomic Qubits,” D. Matsukevich, P. Maunz, D. L. Moehring, S. Olmschenk, and C. Monroe, Phys. Rev. Lett. 100, 150404 (2008).
“Manipulation and Detection of a Trapped Yb+ Hyperfine Qubit,” S. Olmschenk, K. C. Younge, D. L. Moehring, D. Matsukevich, P. Maunz, and C. Monroe, Phys. Rev. A 76, 052314 (2007).
“Entanglement of Single-Atom Quantum Bits at a Distance,” D. L. Moehring, P. Maunz, S. Olmschenk, K. C. Younge, D. N. Matsukevich, L.-M. Duan, and C. Monroe, Nature 449, 68 (2007).
“Robust probabilistic quantum information processing with atoms, photons, and atomic ensembles,” L.-M. Duan and C. Monroe, Advances in Atomic, Molecular, and Optical Physics, vol. 55, E. Arimondo, P.R. Berman and C.C. Lin, eds. (Elsevier, 2007), pp. 419-464.
“Quantum Interference of Photon Pairs from Two Remote Trapped Atomic Ions,” P. Maunz, D. L. Moehring, S. Olmschenk, K. C. Younge, D. N. Matsukevich and C. Monroe, Nature Phys. 3, 538 (2007).
“Quantum Networking with Photons and Trapped Atoms (Invited)“, D. L. Moehring, M. J. Madsen, K. C. Younge, R. N. Kohn, Jr., P. Maunz, L.-M. Duan, C. Monroe, and B. B. Blinov, J. Opt. Soc. Am. B 24, 300 (2007).
“Probabilistic Quantum Gates between Remote Atoms through Interference of Optical Frequency Qubits“, L.-M. Duan, M. J. Madsen, D. L. Moehring, P. Maunz, R.N. Kohn, Jr., and C. Monroe, Phys. Rev. A 73, 062324 (2006).
“Ultrafast Coherent Excitation of a Trapped Ion Qubit for Fast Gates and Photon Frequency Qubits“, M. J. Madsen, D. L. Moehring, P. Maunz, R. N. Kohn, Jr., L.-M. Duan, and C. Monroe, Phys. Rev. Lett. 97, 040505 (2006).
“Experimental Bell Inequality Violation with an Atom and a Photon“, D. L. Moehring, M. J. Madsen, B. B. Blinov, and C. Monroe, Phys. Rev. Lett. 93, 090410 (2004)
“Scalable Trapped Ion Quantum Computation with a Probabilistic Ion-Photon Mapping“, L.-M. Duan, B. B. Blinov, D. L. Moehring, and C. Monroe, Quant. Inf. Comp. 4, 165 (2004)
“Observation of Entanglement Between a Single Trapped Atom and a Single Photon“, B. B. Blinov, D. L. Moehring, L.-M. Duan, and C. Monroe, Nature 428, 153 (2004)
“The Trap that Russ Built“, by Boris Blinov