Our group has several research projects involving various aspects of controlling trapped atomic ions and individual photons for quantum information purposes. Active projects include research of
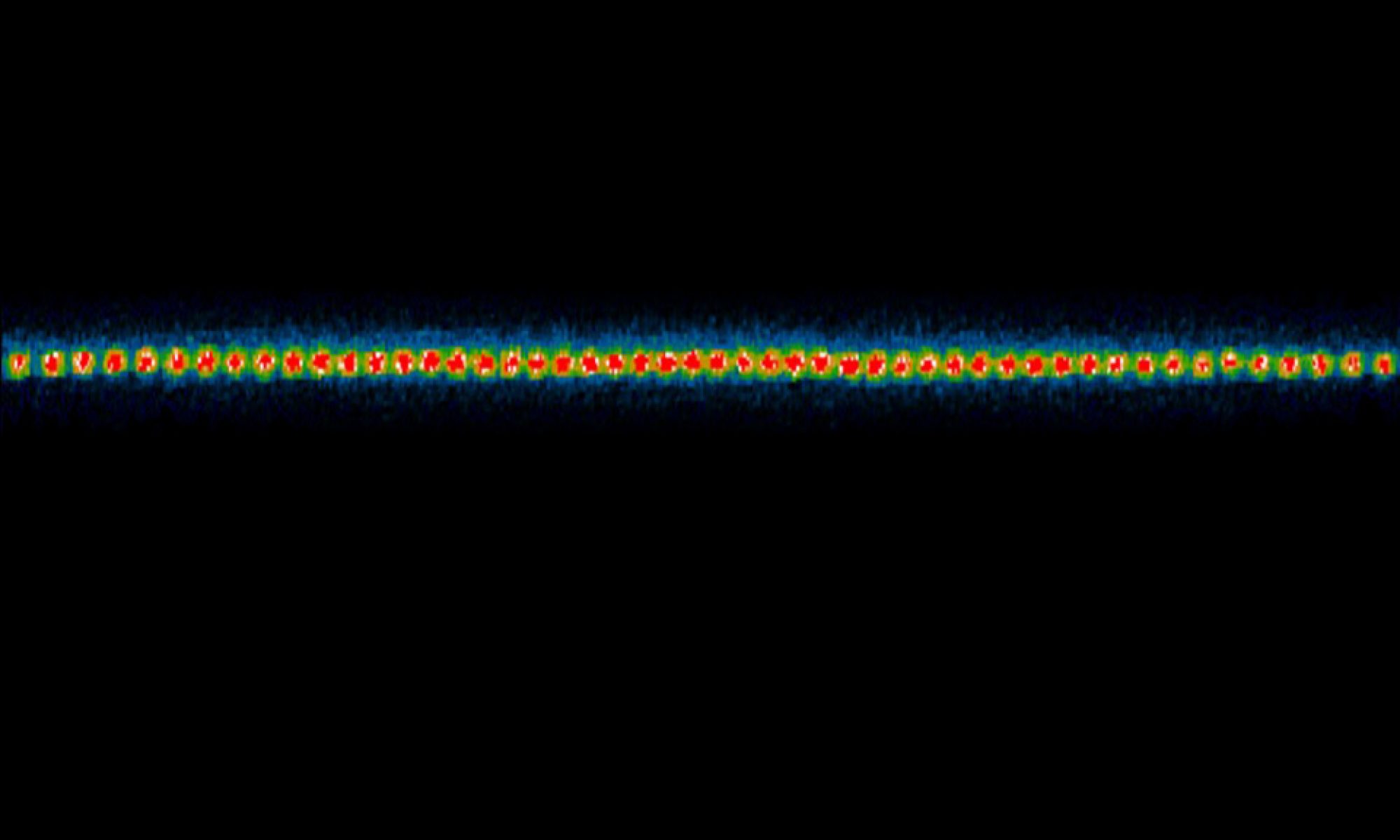

Trapped Ion Quantum Information
CHRISTOPHER MONROE, Principal Investigator. University of Maryland Department of Physics, Joint Quantum Institute, and Center for Quantum Information and Computer Science