About our experiment
Originating in large part with Richard Feynman’s 1982 proposal, quantum simulation has evolved into a field where scientists use a controllable quantum system to study a second, less experimentally feasible quantum phenomenon. In short, a full-scale quantum computer does not yet exist and classical computers often cannot solve quantum problems, thus a “quantum simulator” presents an attractive alternative for gaining insight into complex material properties, for example.
Can a quantum simulator provide solutions to physics or computation problems that cannot be tackled using conventional computers? The quantum simulation lab uses an apparatus that lays the groundwork necessary to undertake this challenging question. In ion trap experiments, physicists can have exquisite control of otherwise fragile quantum states, making this platform ideal for simulations.
This lab starts by encoding the transverse field Ising model Hamiltonian onto a chain of ytterbium ions. The Ising model is perhaps the most simple of the spin models, and yet is believed to represent a good description of physical phenomena ranging from ferromagnetism to frustration in spin glasses, and even neural networks. When an external magnetic field is added to the bare spin-spin coupling, quantum properties come into play. One goal is to engineer any spin (magnetic) model, such that we might probe different types of complex phenomena.
The Ising model with a transverse field also has a computation angle: for some cases discovering the lowest energy configuration or ground state is classified as an “NP-complete” problem. This famous class of problems cannot be efficiently solved using conventional computers, with the most popular example being the “traveling salesman problem” of discovering the shortest route through a number of cities on a map. While properties of this finite spin system can be calculated, we are, as a group, fast approaching the number of spins wherein calculations of system properties will be impossible even with state-of-the-art computing technology.
————————————————————————————————-
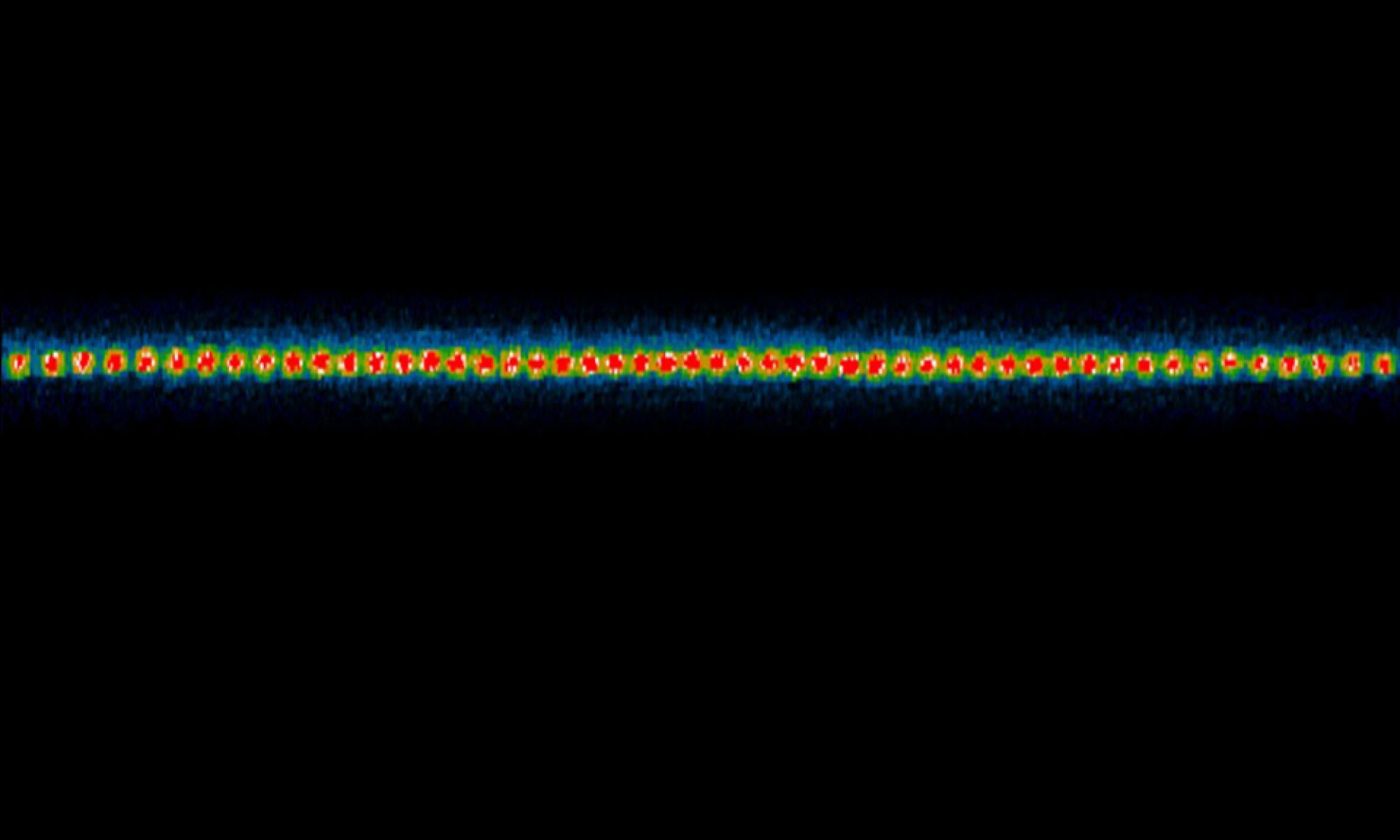
The qubits are represented by individual atomic ytterbium ions stored in stable internal energy levels, typically hyperfine spin states of the ground electronic configuration. While these effective spins do not interact directly, they can be made to interact through the application of spin-dependent laser forces. For example, when a laser force pushes a single atomic ion up for one qubit state and down for the other qubit state, the ion now has a very strong electric dipole moment — a single charge in two positions. This type of laser force is exactly that used for quantum logic gates in trapped ion quantum computing.
When such a spin-dependent laser force is simultaneously applied to a string of atomic ions, the interactions between this dipolar matter give rise to non-trivial phases of order and disorder in the system. Because the system is composed of a stationary crystal of atoms, we have the capability of measuring every possible spin-spin correlation to track the ground state, characterize various forms of entanglement, or measure dynamics of this coupled spin system. Moreover, the external control of the laser force allows for unprecedented control of form and range of the effective interaction between spins. In some cases the interaction is uniform across all ions; in others it falls of like a typical 1/r³ dipolar decay. We can also simulate almost anything in between. The power of this design is that there is effectively a ‘magnetic interaction control knob’ that we can vary at will. This makes the protocol inherently versatile in that it can be extended to other types of spin models.
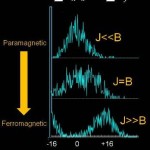
An example sequence for a simulation is as follows: To observe a ferromagnetic transition, a large effective transverse magnetic field overpowers the spin system’s tendency to order. Thus, the spins are in a disordered state. A crossover to ferromagnetism (FM) occurs when this magnetic field is weakened compared to the spin-spin interaction, and all spins are oriented in the same direction. In the quantum regime, the ferromagnet can be prepared in superposition of all spins simultaneously in the up and down state.
There are a rich variety of spin Hamiltonians that can be simulated in the trapped ion system, from the general XYZ spin model to non-trivial multi-dimensional Ising models. As the number of atomic ions in the crystal increases, we expect interesting phenomena to arise, such as ferromagnetism and anti-ferromagnetism over various ranges in the crystal, spin frustration, and “spin-liquid” behavior.
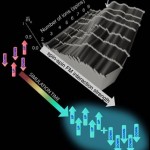
We build up and characterize the simulator in a “ground-up” approach–one spin at a time–which allows us to explore system-size effects, such as how the transition from paramagnetism to ferromagnetism sharpens with each additional particle (see gallery image above). We are also exploring frustrated networks of ion spins and how frustration is related to entanglement. In pushing the limits of the simulator and extending studies beyond ground state phases, we hope to uncover new physics and in the process, understand the true potential of quantum simulators.
While the trapped ion approach deals with small numbers of particles, in the future we will be able to program arbitrary interactions between all pairs of spins. Such a fully-connected set of interacting spins will allow the simulation of systems that can never be understood using conventional computers.
Check out our latest results!
“Many-body localization in a quantum simulator with programmable random disorder,” J. Smith, A. Lee, P. Richerme, B. Neyenhuis, P. W. Hess, P. Hauke, M. Heyl, D. A. Huse, and C. Monroe, arXiv: 1508.07026 (2015).
“Realization of a Quantum Integer-Spin Chain with Controllable Interactions,” C. Senko, P. Richerme, J. Smith, A. Lee, I. Cohen, A. Retzker, and C. Monroe. Phys. Rev. X. 5, 021026 (2015).
“Coherent Imaging Spectroscopy of a Quantum Many-Body Spin System,” C. Senko, J. Smith, P. Richerme, A. Lee, W.C. Campbell, and C. Monroe, Science 345, 430 (2014). [Supplementary Information]
“Non-local propagation of correlations in quantum systems with long-range interactions,” P. Richerme, Z.-X. Gong, A. Lee, C. Senko, J. Smith, M. Foss-Feig, S. Michalakis, A. V. Gorshkov, and C. Monroe, Nature 511, 198 (2014).
“Quantum Catalysis of Magnetic Phase Transitions in a Quantum Simulator,” P. Richerme, C. Senko, S. Korenblit, J. Smith, A. Lee, R. Islam, W. C. Campbell, and C. Monroe, Phys. Rev. Lett. 111, 100506 (2013).
“Experimental Performance of a Quantum Simulator: Optimizing Adiabatic Evolution and Identifying Many-body Ground States,” P. Richerme, C. Senko, J. Smith, A. Lee, S. Korenblit, and C. Monroe, Phys. Rev. A 88, 012334 (2013).
“Emergence and Frustration of Magnetism with Variable-Range Interactions in a Quantum Simulator,” R. Islam, C. Senko, W. C. Campbell, S. Korenblit, J. Smith, A. Lee, E. E. Edwards, C.-C. J. Wang, J. K. Freericks, and C. Monroe, Science 340, 583 (2013). [Supplementary Material]
“Quantum Simulation of Spin Models on an Arbitrary Lattice with Trapped Ions,” S. Korenblit, D. Kafri, W. C. Campbell, R. Islam, E. E. Edwards, Z.-X. Gong, G.-D.Lin, L.-M. Duan, J. Kim, K. Kim, and C. Monroe, New J. Phys. 14 095024 (2012).
“Quantum Simulation of the Transverse Ising Model with Trapped Ions,” K. Kim, S. Korenblit, R. Islam, E. E. Edwards, M.-S. Chang, C. Noh, H. Carmichael, G.-D.Lin, L.-M. Duan, C.-C. Joseph Wang, J. K. Freericks, and C. Monroe, New J. Physics 13, 105003 (2011).
“Onset of a Quantum Phase Transition with a Trapped Ion Quantum Simulator,” R. Islam, E. E. Edwards, K. Kim, S. Korenblit, C. Noh, H. Carmichael, G.-D.Lin, L.-M. Duan, C.-C. Joseph Wang, J. K. Freericks, and C. Monroe, Nature Communications 2, 377 (2011).
“Quantum simulation and phase diagram of the transverse-field Ising model with three atomic spins,” E. E. Edwards, S. Korenblit, K. Kim, R. Islam, M.-S. Chang, J. K. Freericks, G.-D. Lin, L.-M. Duan, and C. Monroe, Phys. Rev. B 82, 060412 (2010).
“Quantum Simulation of Frustrated Ising Spins with Trapped Ions,” K. Kim, M.-S. Chang, S. Korenblit, R. Islam, E. E. Edwards, J. K. Freericks, G.-D. Lin, L.-M. Duan, and C. Monroe, Nature 465, 590 (2010).
“Entanglement and Tunable Spin-Spin Couplings between Trapped Ions Using Multiple Transverse Modes,” K. Kim, M.-S. Chang, R. Islam, S. Korenblit, L.-M. Duan, and C. Monroe, Phys. Rev. Lett. 103, 120502 (2009).